ファン・デル・ワールスの状態方程式が描くグラフにおいて、臨界温度より低い温度で極値を持つ曲線の場合、点 A より右側では気体として存在し、点 E より左側では液体として存在していると言えます。 マクスウェルの等面積則. では、点線の位置はどのように決まるのでしょうか。 この点線の位置がどこでもよければ、同じ温度でも、気体から液体に変わるときの圧力がバラバラになってしまいます。 したがって、点線の位置をどこかに決めるルールが必要です。 これについてはマクスウェルの等面積則という、ありがたいルールがあります。 マクスウェルの等面積則では、ABC で囲まれた面積と CDE で囲まれた面積が等しくなるように点線を引くこととなっています。 このルールにしたがうと、点線を引く位置は1つに定まります。. 理想気体温度計：理想気体では、圧力p、体積V、モル数n、気体定数R (= 8.31 J/K mol)]、 温度 T として、ボイルシャルルの法則 pV = nRT が成り立つ。 一定圧力下における膨張を温度計とみなす

ファンデルワールスの状態方程式について丁寧に解説！【大学の物理化学】 YouTube

内部エネルギー

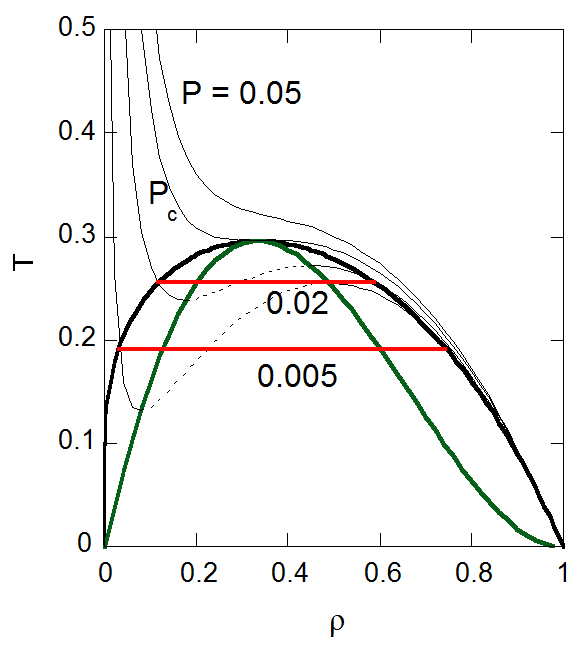
ファンデルワールス状態方程式のはなし：ファンデルワールス流体の気液平衡

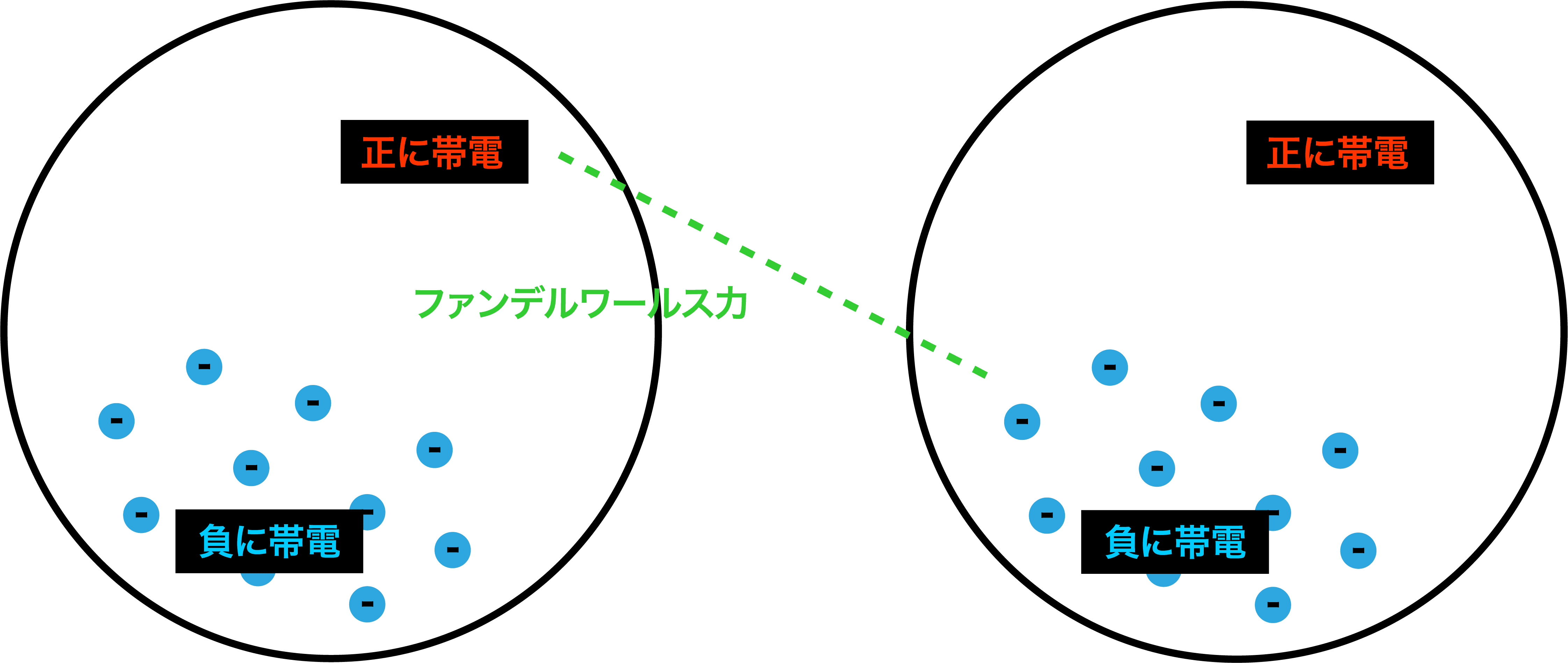
分子間力（水素結合・ファンデルワールス力・沸点のグラフなど） 化学のグルメ

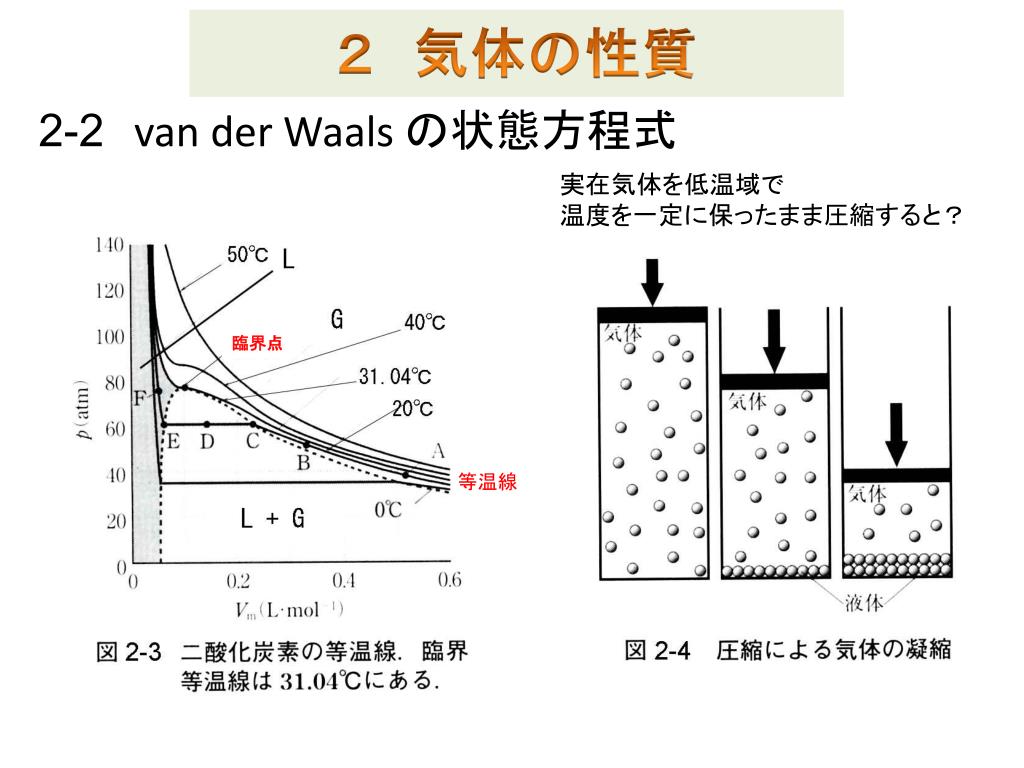
PPT 医薬品素材学 I PowerPoint Presentation, free download ID4849100

ファン・デル・ワールスの状態方程式（クラウジウス=クラペイロンの式、ジュール=トムソン効果）

ファンデルワールス力と状態方程式 理系ラボ

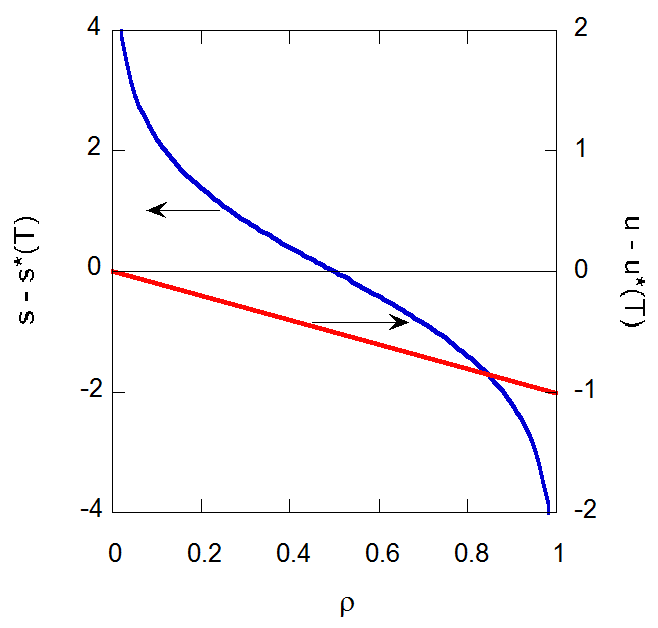
ファンデルワールス状態方程式のはなし：エントロピーからの視点

ファンデルワールスの状態方程式 / 汚泥乾燥機, スラリー乾燥機, ヒートポンプ汚泥乾燥機 KENKI DRYER

気体の状態方程式 monozukurihitozukuri 日本のものづくり

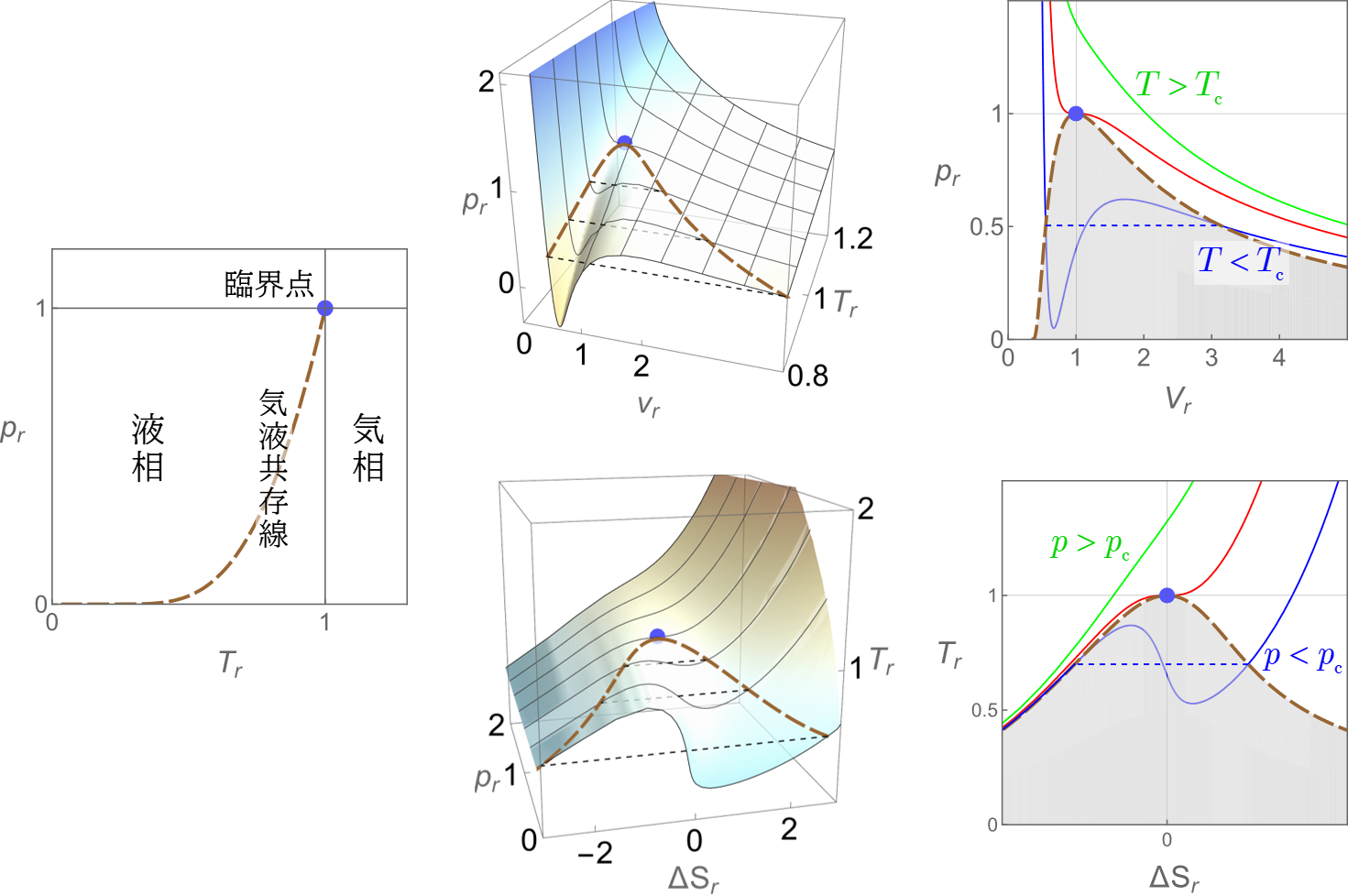
ファン・デル・ワールス流体

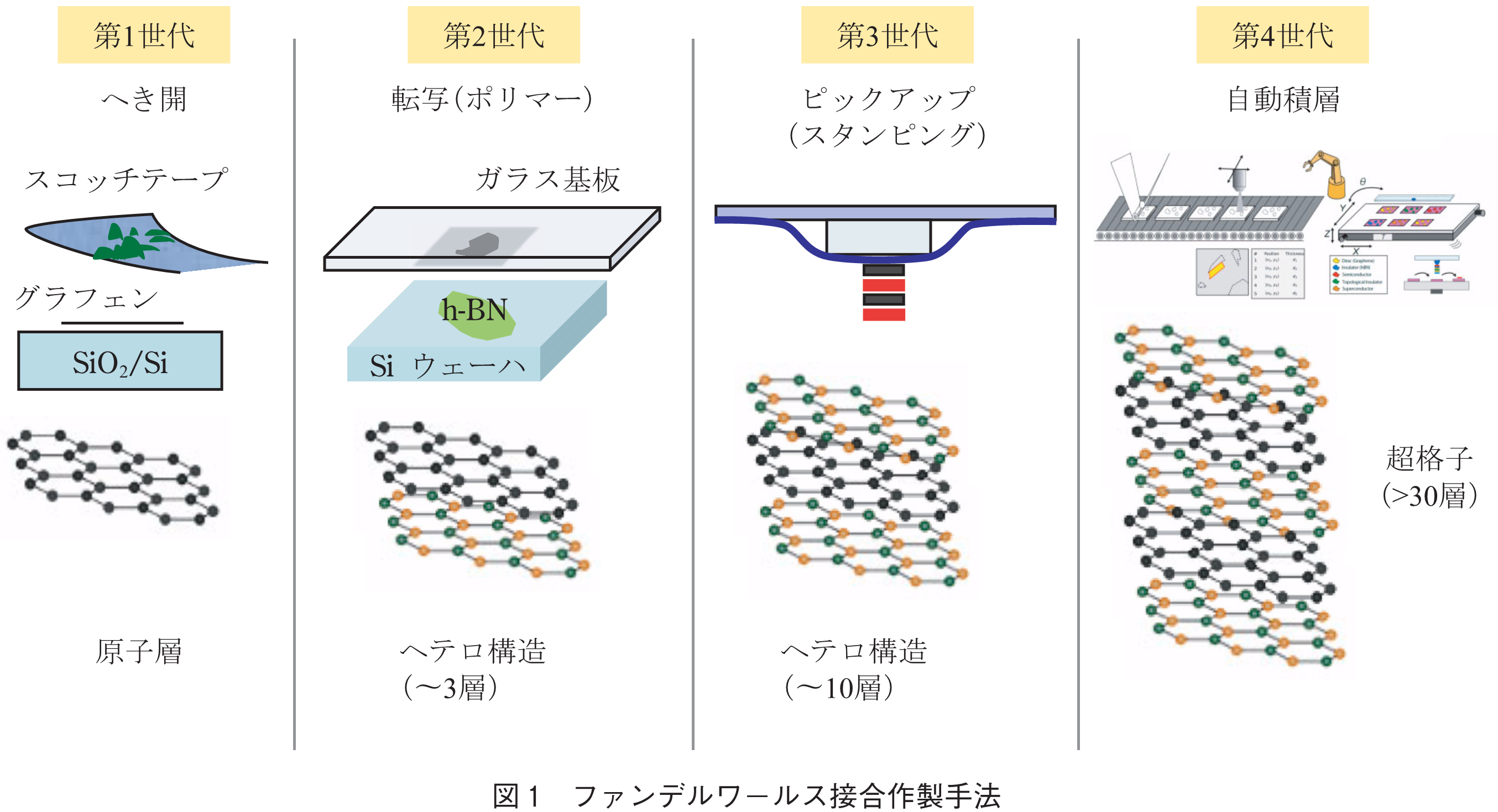
解説 二次元物質ファンデルワールス接合の作製技術構築と物性創発

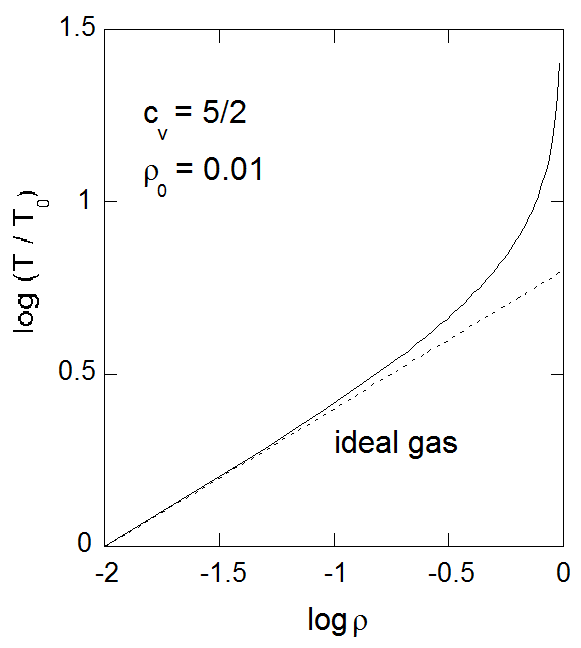
ファンデルワールス状態方程式のはなし：エントロピーからの視点

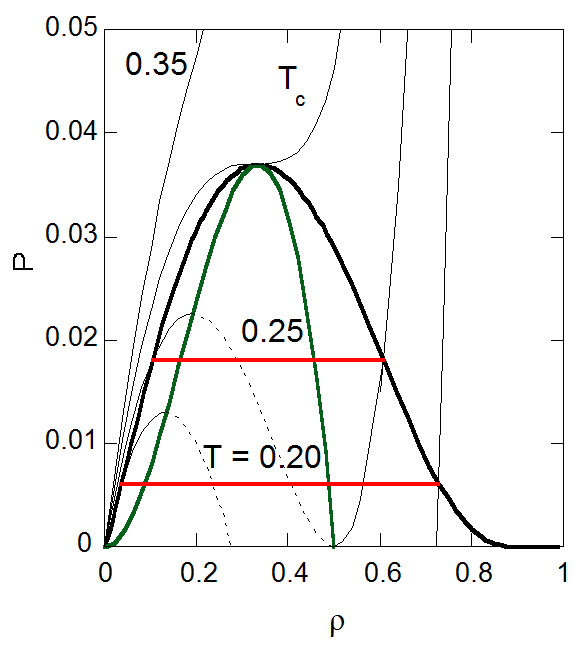
ファンデルワールス状態方程式のはなし：ファンデルワールス流体の気液平衡

ファン・デル・ワールス方程式｜理想気体よりも実在の気体に近い Hitopedia

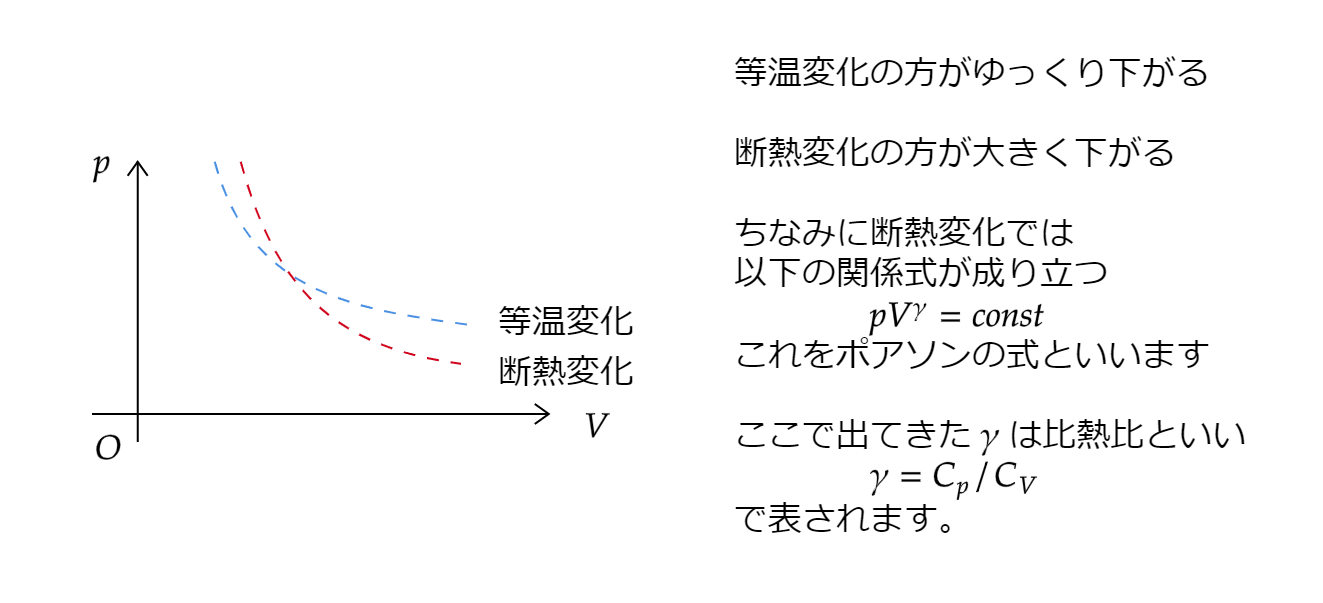
23気体の内部エネルギー・比熱 受験の物理屋さん

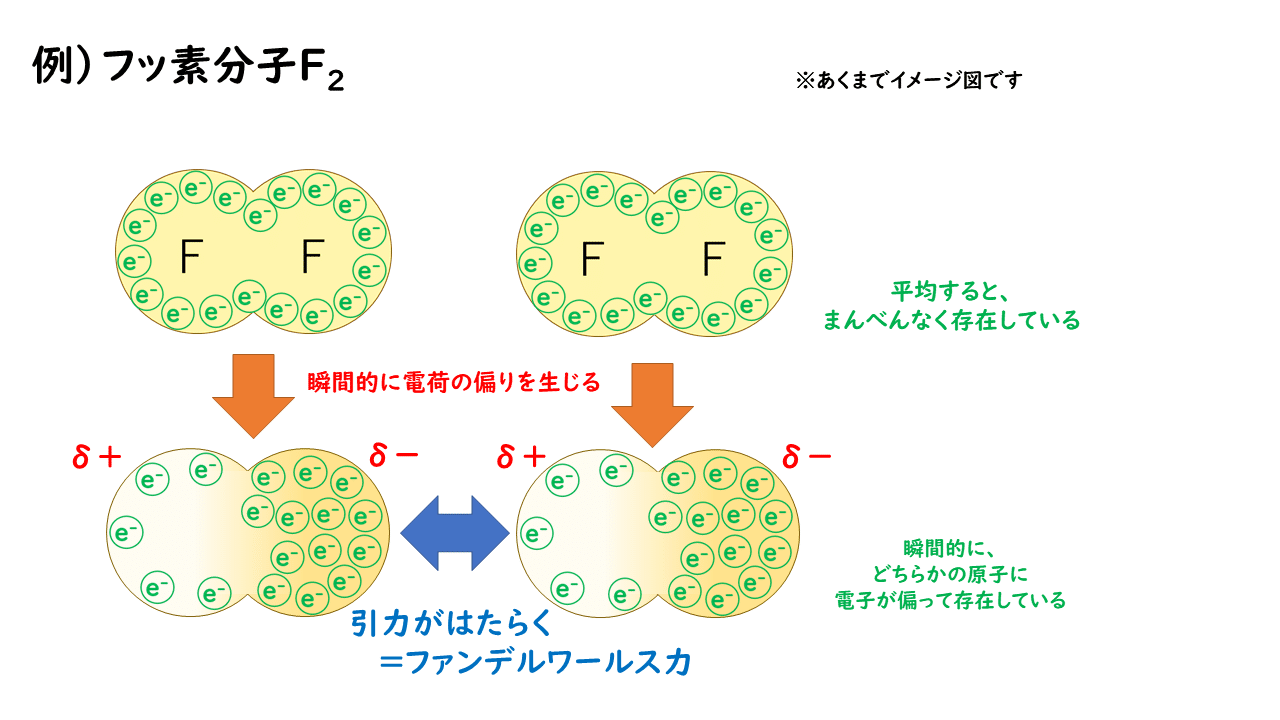
分子 間 力 ファン デル ワールス 力 違い

個人的まとめ 問 ファンデルワールスの状態方程式

実在気体－3｜ファン・デル・ワールスの状態方程式が描くグラフの見方｜理系への道

3分で簡単ファンデルワールス力！分子間の相互作用とは？理系大学院卒ライターがわかりやすく解説 ページ 2 StudyZ

この振動はファンデルワールスのループと呼ばれ、非現実的な挙動であるため、その領域を水平線で置き換えるマクスウェルの構成法と呼ばれる操作を行います。. ファンデルワールス方程式 はその一例であり次式で与えられます。 P = \frac {nRT} {V - nb} - a \left ( \frac {n} {V} \right)^2 P = V −nbnRT −a(V n)2. ここで a a は分子間相互作用パラメータ、 b b は1分子の体積を表しています。 目次 . 1.実在気体. 2.実在気体の理想からのズレを数値化する : 圧縮率因子. 3.実在気体の状態方程式 : ファンデルワールス方程式. 4.圧縮率因子の挙動と原因. 4-1.圧縮率因子が1より小さくなる原因. 4-2.圧縮率因子が1より大きくなる原因. 5.実在系が理想的に振る舞う温度 : ボイル温度. 実在気体.