Least Common Multiple (LCM) of 8 and 10 with Primes. Least common multiple can be found by multiplying the highest exponent prime factors of 8 and 10. First we will calculate the prime factors of 8 and 10. Prime Factorization of 8. Prime factors of 8 are 2. Prime factorization of 8 in exponential form is:. The second method to find LCM for numbers 8 and 10 is to list out the common multiples for both nubmers and pick the first which matching: Multiples of 8: 8, 16, 24, 32, 40, 48, 56 . Multiples of 10: 10, 20, 30, 40, 50, 60 . So the LCM for 8 and 10 is 40

LCM of 8 and 10 How to Find LCM of 8, 10?

Common Multiples Chart Framework Montessori

Ex 3.4, 1 Find first three common multiples of Class 6 Teachoo

Common Multiples Definition Properties Formulas Solve vrogue.co

PPT Factors & Multiples PowerPoint Presentation, free download ID1465198

Multiples and Factors Math Original YouTube

Using Multiples of 8 To Know What Least Common Multiple Means Juni Learning

Lowest Common Multiple GCSE Maths Steps & Examples

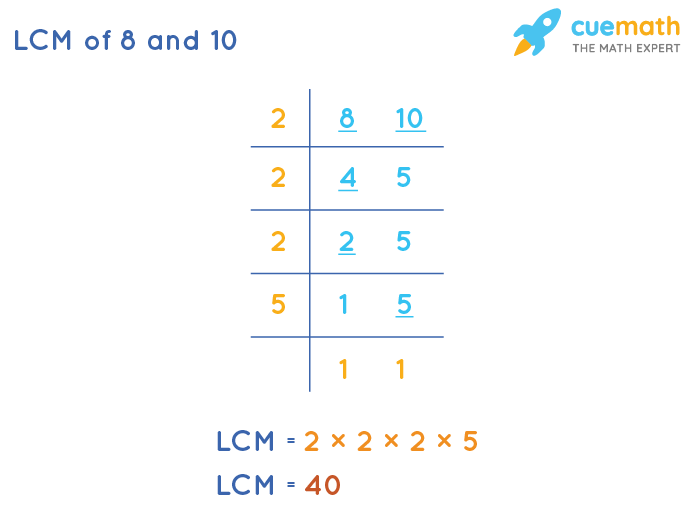
LCM of 8 and 10 How to Find LCM of 8, 10?

Common Multiple — lesson. Mathematics State Board, Class 6.

Common Multiples and Common Factors

What are Common Multiples? Definition, Examples, Facts

Common Multiples — Definition & Examples Expii

Factors and Multiples Math Worksheets Ages 810 Activities

bettersalesweb26 Least Common Multiple Of 8 And 9

Multiples of 8 Maths with Mum

Math Common Multiples YouTube

Common multiple of 8 and 3 What is the lowest common multiple? — WellHouse Church Building His

Maths GCSE Lesson 4 Lowest Common Multiples YouTube

PPT WALT Find the Lowest Common Multiple PowerPoint Presentation, free download ID332976

The Least Common Multiple (LCM) is also referred to as the Lowest Common Multiple (LCM) and Least Common Divisor (LCD). For two integers a and b, denoted LCM(a,b), the LCM is the smallest positive integer that is evenly divisible by both a and b. For example, LCM(2,3) = 6 and LCM(6,10) = 30.. A common multiple of two numbers is a product you can get by multiplying each of the two numbers by some whole number. For example, 30 is a common multiple of 3 and 5, because 3 ⋅ 10 = 30 3 ⋅ 10 = 30 and 5 ⋅ 6 = 30 5 ⋅ 6 = 30. Both of the factors, 10 and 6, are whole numbers. The multiples of 3 are 3, 6, 9, 12, 15, 18, 21, 24, 27, 30.